PEG vobuml--tjl: UML stereotypes for describing Vob structs
| Author: | Tuomas J. Lukka |
|---|---|
| Last-Modified: | 2003-01-01 |
| Revision: | 1.11 |
| Status: | Incomplete |
With PP and hierarchical coordinate systems, the structure of vob scenes' contents (what coordinate systems there are, what vobs there are, how are they connected) is now complicated enough that we need to be able to diagram it easily. This PEG describes some extensions to UML for this purpose.
The idea is that diagrams are kind of a template for actual vobs and coordinate systems. For example, in LinebrokenCellContentView, we have a box cs everything is put into, a translated cs for scrolling when the cursor's not on the first line, one cs for every word (each piece of text is an own vob), and a TextVob for every word. We'd model this by showing four classes, one for every cs and one for the vobs-- so we don't show actual vobs and and coordinate systems, but the kinds of vobs and cs there are in our structure and how they are related.
Issues
Should Coordinate systems use the generalization relationship to their type? I.e. "coordinate system of viewport frame inherits from orthoboxCS"?
RESOLVED: No. In the current context, the coordinate system type is a metaclass, not a parent class. While a template might be considered, the template notation is clumsy. Therefore, we shall use the stereotype notation for coordinate systems: defining stereotypes such as "orthoboxCS" for all coordinate system types, and "*CS" for coordinate systems of indeterminate type.
Should we define images for the Vob and Coordsys stereotypes?
RESOLVED: Not yet.
How should the interpolation key be represented?
How should the sequence of Vobs be shown? Specifically, if there are alternatives (e.g. in Stencil, the border may be left out). UML statechart -type things?
How strict should the order grouping be? Do we need to be able to express "this immediately before that"?
Should this spec discuss umltool as well?
RESOLVED: Besides giving clear names to the relationships, no.
How to distinguish between parent roles and multiplicities? E.g. "there are n content coordinate systems".
RESOLVED: numbers should not be used for parent roles; if nothing else, parent0, parent1 should be used.
The objects to be described
There are two kinds of "objects" (in the following, the quotes will be dropped) in the Vob system: coordinate systems and vobs. OpenGL adds another distinction: GL state -changing vobs and rendering vobs.
The main relationships for coordinate systems are:
- Transform parenthood (DAG: n*Coordsys - n*Coordsys (ordered))
- Interpolation parenthood (TREE: n*Coordsys - Coordsys)
- Interpolation (BIPARTITE GRAPH: Coordsys - Coordsys in other VobScene)
And for Vobs,
Vob containment (BIPARTITE GRAPH: n*Vob - n*Coordsys (ordered))
Vob order (SEQUENCE / PARTIAL ORDER)
The real, physical Vob order is a strict sequence, but when drawing a diagram it can be helpful to only show the meaningful order relations ("A before B, but it doesn't matter when C is drawn")
and the main attributes of coordinate systems are
- Type
- Interpolation key
and for Vobs,
- Type
- Parameters
Vob-UML
Both coordinate systems and Vobs are represented as stereotyped UML classes. For coordinate systems, stereotypes ending in CS are used, and for Vobs, Vob or one of Vob0, Vob1 and Vob2 is used (for vobs with zero, one or two vobs, respectively).
Relationships between coordinate systems
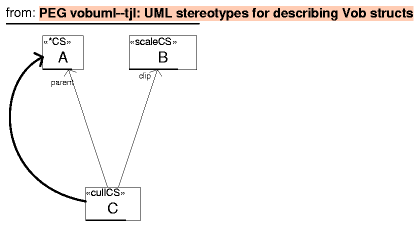
Both types of relationships between coordinate systems in the same VobScene are represented as arrows; the arrow for transform parenthood (A vobtransform B == A is child of B) is thin and possibly contains (at the arrow end) the name of the parent's role. The interpolation parenthood (A vobsubmatch B == A is interp child of B) is represented by a thick arrow.
In the above diagram, there are three coordinate systems, and the corresponding code would be approximately (A given as parameter):
B = vs.coords.scale(0, ...) C = vs.coords.cull(A, B) vs.matcher.addSub(A, C, ...)
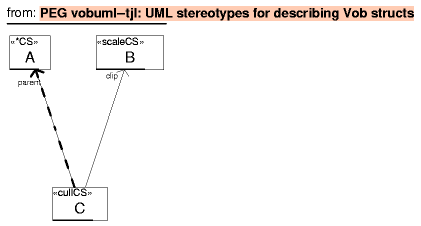
Since the same two coordinate systems often have both vobsubmatch and vobtransform relationships, a visual shorthand of dashing the line types can be used:
Relationships of Vobs
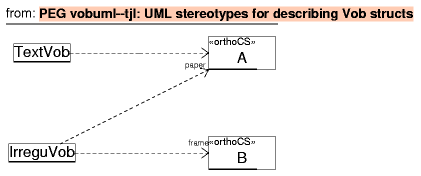
The containment of a Vob in coordinate system(s) (A vobin B == Vob A is in CS B) is represented by a thin, dashed line. The coordinate system end is optionally adorned by the index.
In the above diagram, there are two Vobs and two coordinate systems. The TextVob is placed in A, and the IrreguVob, which uses two coordinate systems, is in A and B.
Examples
One relatively complex example is the stenciling of irregular coordinate systems. There, the sequence is:
- Vob to set OpenGL Stencil state
- Vob in frame coords to draw the stencil
- Vob to set OpenGL Stencil state
- Vob in frame coords to draw the edge outside the stencil
- Vob to set OpenGL Stencil state
- Vob to draw contents in contents coordinate system
- Vob to set OpenGL Stencil state
- Vob in frame coords to draw the stencil + possibly more, if faster
- Vob to set OpenGL Stencil state